You didn’t expect this to be simple, did you?
Author’s note: This article ended up being “crowdsourced” through helpful (and accurate) criticism in the comments section. The Excel formulae have been edited to reflect these better techniques. Read the comments section for more great ideas.
By David Enna, Tipswatch.com
Although I have been investing in I Bonds for more than 20 years and have been writing about them for 11 years, I never paid much attention to the “exact” way interest is calculated. I figured, I’ve got a $10,000 I Bond earning 9.62%, so in six months I’d earn $481. Close enough, right?
But if you use TreasuryDirect’s Savings Bond Calculator you may notice very slight discrepancies, even after accounting for the three-month early withdrawal penalty. The Treasury’s interest calculation is ridiculously complex and possibly a relic of ancient times when $25 savings bonds were a thing.
I don’t think TreasuryDirect ever explicitly explains the complex process, but here is a good explanation of the I Bond interest calculation from the Bogleheads Wiki:
How interest is calculated
All bond values are based on the $25 bond. A $5000 bond is worth 200 times what a $25 bond is worth; a $100 bond is worth 4 times what a $25 bond is worth. If you have a $80 electronic bond at TreasuryDirect, it is worth 3.2 $25 bonds. The $25 bond value is always rounded to the nearest penny. Thus, a $5000 bond must always have a value that is a multiple of $2.00.
Interest is computed on a $25 bond using the composite rate divided by 2 for the given six month period. For individual months within the six month period, interest is computed using pseudo-monthly compounding to produce the same result after six months. For example, if the composite rate is 2.57%, the bond value after 1 month is $25 × (1 + 0.0257/2)^(1/6) = $25.05, and after 4 months is $25 × (1 + 0.0257/2)^(4/6) = $25.21, and after 6 months is $25 × (1 + 0.0257/2)^(6/6) = $25.32.
The values of a $100 bond would be $100.20, $100.84, and $101.28 after those same time periods. Note that this ignores the 3 month penalty for redemption within the first 5 years and the restriction on redemption within the first year.
You have to love the term “pseudo-monthly compounding” and you’d have to be a genius to apply these formulae to your holdings. I mean, what the heck is a ^? But the key factor is that the interest is applied to $25, rounded to the nearest penny, then scaled up to match your current I Bond holding.
If you bought $10,000 in an I Bond dated May 2022, this would be the formula you’d use in Excel to determine the value for the first month, effective on the first day of the month after your purchase: =ROUND(25*(1+0.0962/2)^(1/6),2) . The second month would be =ROUND(25*(1+0.0962/2)^(2/6),2) . The result for month one is $25.20 and multiply that by 400 to get the investment value of $10,080. For month two it is $25.39 for a value of $10,156. I worked my way through Excel to produce this for an I Bond purchased in May 2022:
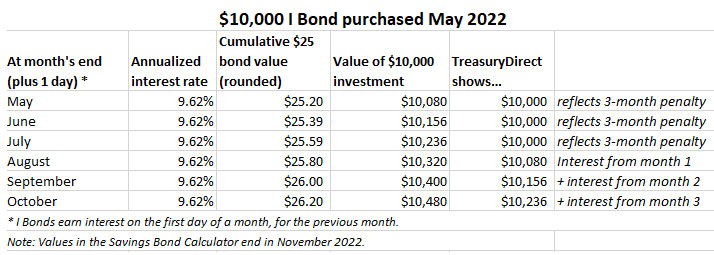
Note: What is the ROUND factor? This came from feedback from readers. If you want to incorporate rounding to the penny into the “Cumulative $25 bond value” column, you need to add ROUND to the formula, as shown in the above examples. It is important to do this if you plan on incorporating that column’s calculation into an additional formula, because this is how the Treasury does its calculations.
Read the comments section for other helpful suggestions from Excel nerds.
I used TreasuryDirect’s Savings Bond Calculator to double-check these value amounts and the October amount (actually the value on November 1) did match the total of $10,236, which is the way TreasuryDirect reports values, minus the three-month interest penalty for early redemptions. Here it is, with a $1,000 investment shown because TreasuryDirect’s calculator is for “paper I Bonds only” and won’t allow an investment input of more than $5,000.

But the tougher question and still a “great unknown” is what happens after six months, when the I Bond’s balance compounds? I couldn’t find a single source that could explain the exact formula. So I devised on of my own. It works, but it could be wrong. Ponder that, math teachers.
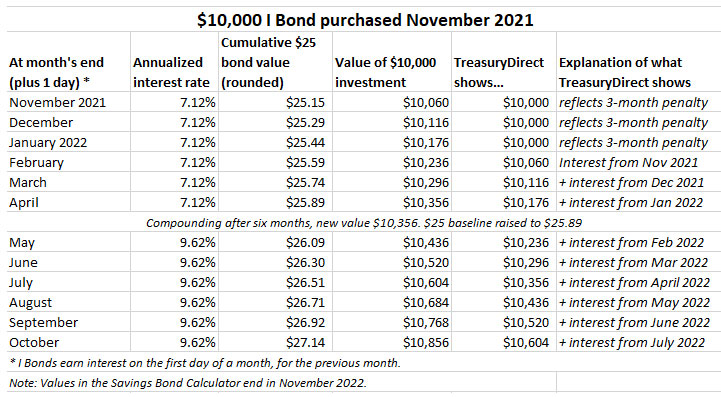
Here is the calculation for an I Bond purchased in November 2021, earning 7.12% for six months and then 9.62% for six months.
In this calculation, I updated the baseline $25 to a value of $25.89 and the new formula for May became =ROUND(25.89*(1+0.0962/2)^(1/6),2) . The formula for June is =ROUND(25.89*(1+0.0962/2)^(2/6),2) . And so on. Using this formula, I was able to match TreasuryDirect’s last estimate of value, which is for October on my chart but actually for November 1. (I Bond interest is earned on the first day of the month for the previous month.)
As a triple-check, I confirmed my calculations for the May 2022 I Bond values and November 2021 I Bond values on the EyeBonds.info site, which is as rock solid as any information you will find. My numbers matched up with that site’s findings.
Don’t forget …
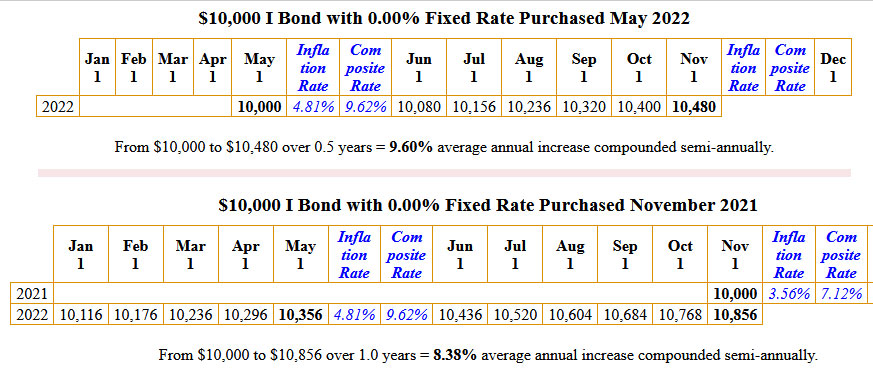
Until your I Bond investment reaches 5 years, TreasuryDirect will always show the current value minus the latest three months of interest. You have earned that interest, but TD won’t show it to you, because if you sold out today, you’d get the amount they indicate.
In the case of the November 2021 purchase, that $10,000 I Bond is actually worth $10,856, even if TD shows you $10,604.
A Tip of the Hat to Jennifer Lammer
Lammer, CEO of Diamond NestEgg, is a YouTube video star who offers some well-explained, well-documented advice on I Bonds and other investments. She created this video to explain the complexities of I Bond interest payments and the very strange $25 baseline for all investments.
Her worksheet calculations don’t match mine — we used different starting months — but we come up with similar results, which as I love to note, would drive math teachers crazy. There is a lot of good information in this video, and Lammer makes a valiant effort to make something very complex sound simple. If anyone has further advice on this I Bond calculation, send it my way in the comments section below.
• Confused by I Bonds? Read my Q&A on I Bonds
• Inflation and I Bonds: Track the variable rate changes
• I Bond Manifesto: How this investment can work as an emergency fund
* * *
Feel free to post comments or questions below. If it is your first-ever comment, it will have to wait for moderation. After that, your comments will automatically appear.
David Enna is a financial journalist, not a financial adviser. He is not selling or profiting from any investment discussed. The investments he discusses can be purchased through the Treasury or other providers without fees, commissions or carrying charges. Please do your own research before investing.



Thanks for this helpful breakdown of the interest calculation! Thanks to this I was able to implement it into a model for calculating the effective yield one would earn upon redemption of the bond, including any applicable early redemption penalty for <5 years. The interest calc proved to be a lot less intuitive than I would have imagined, but I think this formulation generalizes it enough to be able to calculate redemption values at any given date. Happy to hear any feedback. https://docs.google.com/spreadsheets/d/1_CaGeG9KXKcdeV0EuSRwQOfud8Gozd5px73orl18A1g/edit?usp=sharing
Regarding I-bond calculation methodology.
Hey, you don’t have to understand much if any of the algebraic math, that’s what spreadsheets are for. But compounding rules are fairly universal, and the Treasury doesn’t use anything exotic. Here’s my take on what the exact Treasury “rules” are for their I-bond calculations (BTW, there are no $25 denomination I-bonds, so it muddies the water to even talk about something fictitious) These calculations have been tested for I-Bond values as listed in the Treasury Savings Bond Calculator for a 23 year period, beginning December 2000, and always have given the exact redemption values, to the penny. I wrote this originally in June of 2022, have only modified the wording since.
——
A) Interest rate applicable
I = Fixed rate +2*Variable rate + Fixed rate*Variable rate= Composite interest rate
This interest rate is applied for 6 months, starts with the month you purchased the bond in, and changes every 6 months after that date.
For example, I purchased some bonds in December 2000, which had a fixed rate of 3.4% (.034) and every 6 months beginning in December or June for this particular bond the new composite rate will be applied. The CPI announced for the 6 months ending in March 2022 was 4.81% (.0481). So Composite rate now is I= .034+2*.0481+.034*.0481=.1318 (round to 4 decimal places). This is an annual rate of 13.18%. Highest rate ever! It changed in June, and a new rate will become applicable in December 2022.
To calculate the monthly change in bond value increments, first divide the composite annual rate by 2 to get the 6 month rate, then add 1 and take the 6th root. (use the spreadsheet formula for taking roots) So for July 2022 the monthly factor will be (1+(.1318/2)) to the 1/6 power= 1.010693355… This is the monthly factor for calculating bond value increments, for bonds purchased in December 2000, for each of the 6 months starting in June 2022. Multiply the current value by this factor to get the new monthly value for next month. (see next section about bond values and rounding off)
B) Round off rules for calculating bond values in increments of 40 cents for paper bonds follow. (Electronic bonds most likely have similar rules, with only slight round-off differences, but I have not investigate them)
FOR PAPER BONDS ONLY: If you bought paper bonds, each bond will have values in 40 cent increments. Multiply the initial value of the bond purchased by 2.5. This will always give an even number of 40 cent increments since paper bonds can only be purchased in amounts of $50, $100, $200, $500, or $1000. In my example the $1000 bond value, which was initially 2500 increments in December 2000, totaled 8371 increments=$3348.40 as of June 2022, so the new value of increments (UNROUNDED) for July 2022 is 1.010693355*8371=8460.514075 of 40 cent increments
The calculation of monthly value above resulted in an uneven number, and the UNROUNDED value is carried forward in the spreadsheet every month as the starting point to be used in the calculation of a new monthly value EXCEPT after the last month of a 6 month cycle. In the 6th month of a cycle the number of increments of bond value is rounded off to an even number, and this new ROUNDED value is used to start the next 6 months of calculations. However, the REDEMPTION VALUE for any month is always rounded to an even number of 40 cent increments. You just round off the number of increments first and then multiply by 40 cents. The interest earned is the difference between monthly values.
I’m not a You-Tube star but I would be interested to hear if any readers find this explanation helpful.
I appreciate your explanation, but the method described in this article is accurate. Maybe your method is also accurate. And yes, $25 I Bonds do actually exist and are the starting point for interest calculations, as described in the Bogleheads wiki: https://www.bogleheads.org/wiki/I_savings_bonds “All bond values are based on the $25 bond.”
It would be clearer to start your post by using the same terms as on the Treasury web site.
The fed’s definition of the Composite interest rate is: Fixed rate + (2 x semiannual inflation rate) + (fixed rate x semiannual inflation rate).
But saying this is your interest rate for the first six months is vague.
The composite rate is the simple interest that will be collected after six months. Period.
Yes, it can, and apparently is, reverse engineered into a compounded-monthly formula. But the effective monthly interest rate has to be lower than the composite rate for the math to work.
I missed this part in economics but thanks to s.m am well sorted now
Pingback: Demystifying I Bonds: A Guide to Inflation-Linked Savings Bonds - He Knows Finance
I read many of the comments but didn’t see this addressed (if it was, apologies!). Since the interest isn’t compounded daily, I’m assuming it makes sense to be strategic as to WHEN in a month one would redeem one’s i-bonds. For example, in order to not lose a full month of interest, it makes sense to redeem on the 2nd of the month (so as to receive the last month’s interest) but not have money sitting there for no reason as redeeming mid or late month would result in no additional interest? For reference, I purchased all of my i-bonds on the 1st of the month. Thanks in advance for any insight!
Doesn’t matter – the interest paid is determined as the last day of the previous month. I.e. bonds cashed anytime in May are redeemed with April interest…
” bonds cashed anytime in May are redeemed with April interest…”
Exactly. So sell early in the month so you can redeploy the proceeds in another asset that makes you interest – even if it’s just a high yield savings account. Because…
Similarly to selling, bonds purchased any time in May earn interest for the full month.
So, sell early in the month – buy late in the month – keep the cash in high yield savings accounts in between.
From what I gather, yes, cash in early in the month as no extra interest is being gained until you get to the next calendar month.
And on the purchase side of things, buy at the end of the month as the bond is backed dated by the Treasury to the first of the month. From the Treasury Direct web site: “I bonds earn interest from the first day of the month you buy them.” So buying on the first of the month is not in your best interest. (Sorry about the pun.)
In the last decade this didn’t matter much, since your money earned 0.0%. Now it is worth the effort; your strategy is correct.
First, super cool explanation on how the I bond interest is computed. It does track with the oddities I saw with my I bond purchase.
However, I am going to take exception to using the term “compounding” of interest that was mentioned in the example Table. The one for a $10K purchase in November of 2021 (“Compounding after six months, new value of $10,356”).
With an interest rate of 7.12%, simple interest on $10K for half a year is exactly $10,356.
There is a “pseudo-appearance” of compounding interest (my words, not yours). Because during the first few months in a the six month cycle you are actually being paid less than the assigned rate of 7.12%. This is then followed by a rate slightly greater than 7.12%, to finish the 6 months with a simple interest rate of 7.12%.
This whole process seemed to be called pseudo-compounding in the article. I agree with the term, in the sense that it falsely gives you the idea that compound interest is involved. You’ll never make more than the simple interest stated. And if you sell early in a six month cycle, you will get a fraction less than the stated rate.
I haven’t read the many comments above, some of which may have addressed my concern, but here it is: The problem I have with the author’s analysis of the arcane TD math is that he compounds the value of the bond monthly – that’s intrinsic to the “pseudo-monthly” thing he uses. This clashes with TD’s assertion that compounding is done only semiannually. My TD results (https://treasurydirect.gov/BC/SBCPrice) are consistent with the summing of each month’s static, non-compounded interest return for a six month accumulation period. That is to say, for example, a $1000 I Bond at an annual 6.48% will earn a monthly interest of $5.60 and after six months will be $33.60 to be added to the $1000 for $1,033.60. At that time the TD’s semiannual compounding will apply the new interest rate to the $1,033.60.
But … this isn’t how it works. There is no I Bond that starts with an interest rate of 6.48%, because anything after Nov 1 is earning 6.89%. So it is tough to correctly examine your premise. So let’s go with a $1,000 I Bond earning 6.89%, purchased in November 2022. At the end of April you would have earned $34.40 interest doled out this way: November $5.60, December $5.60, January $6, February $5.60, March $6 and April $5.60. At that point, you have $34.40 in interest, which is then applied to the new composite rate. It’s a weird system. You can check the results at this page: http://eyebonds.info/ibonds/1000/ib_2022_11.html
Thank you for your comment, but I must point out that my I Bond, purchased 6/2022, earned 9.62% from 6/2022 through 11/2022, at which time the interest was updated to 6.48% starting 12/2022. The TD calculator automatically assigned the correct interest rates. Of course the delayed interest mechanism made the interest only start showing in 10/2022, and the TD calculator showed the $8.00 (for the model $1000 bond) from 10/2022 through 3/2023, but with 11/2022 at $7.60 and 1/2023 at $8.40, which averages to $8.00. Not sure why this happened, but all is well with six months at $8.00 totaling $48.00, in exact agreement with Treasury Direct’s calculator result. Monthly interest = (round (ann. int/1200*25))/25*1000.
If you use the TreasuryDirect calculator, you will always see the correct amount, minus the three-month penalty, if that applies.
Yes, I know that. My going to the TD calculator was to verify that my arithmetic (non-exponential) calculation of monthly interest was consistent with theirs. It is. Not sure why you went to exponential steps (^(1/6, etc.) when the Treasury uses arithmetic operations for monthly I Bond interest. An exponential result can be close only because with small numbers and few steps (maximum six here) exponential increase is close to linear increase, and you can get away with it. For example, 25*1.005^6 = 25.7594, while 25+6*(.005*25) = 25.7500.
David, I must apologize for being apparently unpersuaded before, and to agree now that TD in fact uses the exponential model you presented. I got my “Monthly interest = (round (ann. int/1200*25))/25*1000” from a Jennifer Lammer tutorial, and that method provides a nice, constant monthly return. The Treasury’s method isn’t pseudo-compounding; it really is actual compounding, as they take the sixth root of the current six-month dividend rate +1 and then raising that to the integer of the month (1 through 6), done at the $25.00 level. In my view that has two distinct problems, the first of which is that it is compounding all along, even before the advertised six-month compounding interval. At the $25.00 level, the small increment to be raised to a low number of compounding periods fortunately is trivial, and they can get away with it. The other problem is that the rounding is done at the $25.00 level, so that the resulting rounding error, while trivial at that $25 level, isn’t trivial when the rounded figure is multiplied by 10,000/25 = 400, where the rounding error is similarly multiplied, leading to varying monthly dividend results. No worry, though, as the 6th root of the dividend rate raised to the 6th power is of course the desired dividend rate. Best wishes, Dave Goodridge
This comment for Dave Goodridge comes from Hoyawildcat and I am posting it for him:
Read my comment below, dated Feb 16 2023, that provides a precise and accurate way to calculate the value of any I-Bond in Excel, which is a modification of an earlier and very elegant Excel function created by the user named “Cheers.” (My modified version incorporates fixed rates, which Cheers’s original version didn’t.) This function works, but you need to set up the spreadsheet correctly.
Dave, use whatever formula you like. Here is the complete description from the Bogleheads Wiki on I Bonds:
All bond values are based on the $25 bond. A $5000 bond is worth 200 times what a $25 bond is worth; a $100 bond is worth 4 times what a $25 bond is worth. If you have a $80 electronic bond at TreasuryDirect, it is worth 3.2 $25 bonds. The $25 bond value is always rounded to the nearest penny. Thus, a $5000 bond must always have a value that is a multiple of $2.00.
Interest is computed on a $25 bond using the composite rate divided by 2 for the given six month period. For individual months within the six month period, interest is computed using pseudo-monthly compounding to produce the same result after six months. For example, if the composite rate is 2.57%, the bond value after
1 month is $25 × (1 + 0.0257/2)^(1/6) = $25.05, and after
4 months is $25 × (1 + 0.0257/2)^(4/6) = $25.21, and after
6 months is $25 × (1 + 0.0257/2)^(6/6) = $25.32.
The values of a $100 bond would be $100.20, $100.84, and $101.28 after those same time periods. Note that this ignores the 3 month penalty for redemption within the first 5 years and the restriction on redemption within the first year.
My husband and I sold a family business and now we are no longer working. However, neither one of us are at retirement age and not working. Living off of the sale of the business. Can we still purchase i bonds, eve though we paid no tax?
Yes, definitely.
Ok. Can we purchase the physical bond or do we have to do it electronically. I read something about not being able to purchase them in the physical form. Thank you for the answer.
This is straight from the Treasury Direct website: “Maximum purchase each calendar year: $10,000 in electronic I bonds + $5,000 in paper I bonds”
You can purchase up to $5,000 in paper I bonds (only with your tax refund)
I very much appreciated this article!
It may be worth pointing out to readers that, as Tom H mentioned, the Treasury actually has a pre-computed version of this spreadsheet available for download — more specifically, for the cumulative value of a $25.00 bond. It includes data for both Series I and Series EE bonds, which were issued between May 1992 and today. You just need to filter the rows in the spreadsheet to select the correct bond type and issuance date. (Then of course, multiply these numbers to get the value of an actual bond rather than a $25.00 bond.)
You can download their file here in CSV format:
https://fiscaldata.treasury.gov/datasets/savings-bond-value-files/savings-bonds-value-files
Wow. If it really is available there, your post is extremely helpful. The US Treasury Bond site is the most clunky site I have ever been on. One new thing they now have is the ability to add bank accounts without the pain of having to jump thru the hoops of Medallion signature guarantees. My banks didn’t even know how to do that.
super helpful
Thanks for providing the calculation detail as I was wondering about the amounts I was seeing on my account. If anyone wants an Excel formula to calculate the interest, try this set up:
Enter your issue date in A1 and add one month going down for however many months you have been holding the bond.
Enter your beginning rate in B2 and copy it down to B7. Enter the next rate in B8, and copy down. Keep repeating for however many months.
Enter the amount purchased in C1. Copy the below formula into C2 and drag it down however many months.
=ROUND(ROUND(IF(MOD(COUNT(B$3:B3) + 6, 6) = 1, OFFSET(C3, -1, 0), OFFSET(C3, IF(-MOD(COUNT(B$3:B3),6) = 0, -6, -MOD(COUNT(B$3:B3),6)), 0))/($C$2/25), 2) * POWER(1 + B3/2, IF(MOD(COUNT(B$3:B3) + 6, 6) = 0, 6, MOD(COUNT(B$3:B3) + 6, 6))/6), 2) * ($C$2/25)
Looks very interesting. I tried it, followed your instructions, but I get a “#DIV/0!” error in C2 and in the C column.
I think it’s the “MOD(COUNT(B$3:B3),6)), 0))/($C$2/25), 2)” argument.
My apologies, I added header row mid comment and it pushed the references one row below. This should be the formula:
=ROUND(ROUND(IF(MOD(COUNT(B$2:B2) + 6, 6) = 1, OFFSET(C2, -1, 0), OFFSET(C2, IF(-MOD(COUNT(B$2:B2),6) = 0, -6, -MOD(COUNT(B$2:B2),6)), 0))/($C$1/25), 2) * POWER(1 + B2/2, IF(MOD(COUNT(B$2:B2) + 6, 6) = 0, 6, MOD(COUNT(B$2:B2) + 6, 6))/6), 2) * ($C$1/25)
That works like a champ. Can’t say at the moment whether it’s right, but it works. Nice!
Sorry, but I don’t think your Excel function is correct. I tried to post a detailed reply based on $10K purchased in Oct-21 comparing my results (based on the “magic formula” previously discussed) and yours, but it didn’t take. Go figure….
Interesting, it works for me when I plug my 11/18/21 purchase (11/01/21 issue date) for $10K. My TD account for this purchase is showing a value of $10,768. If I use your example, a 10K purchase on 10/xx/21 would earn 3.54% in the first 6 months, 7.12% in the following, etc. That would be the following inputs:
A1 = 10,000
B2:B7 = 3.54%
B8:B13 = 7.12% and so on
Can you confirm if the value you see in your TD account for this purchase is $10,540?
I mean A1 = 10/1/21 and C1 = 10,000.
For $10K purchased in Oct-21 (B2:B7 = 3.54%, assuming row 1 is a header), then here are the Jan-23 results (C16):
My calculation: $10,792
Your calculation: $11,116
The two calculations agree for the first six months ($10,148 in Apr-22) but diverge after that.
(I have compared my calculation with TreasuryDirect, which reports the totals through Oct-22, i.e. less the three-month interest penalty from Dec-22, and they agree: $10,540 through Oct-22.)
Sorry, Jan-23 results are in C17, with row 1 as a header.
My number agrees with your calculation of $10,792. I think your worksheet might not be set up like mine and it is resulting in an incorrect result.
Assuming no header row, please try the following:
A1 = 10/1/21, A2 = 11/1/21, etc
B1 = Blank, B2:B7 = 3.54%, etc.
C1 = 10,000
C2 = ROUND(ROUND(IF(MOD(COUNT(B$2:B2) + 6, 6) = 1, OFFSET(C2, -1, 0), OFFSET(C2, IF(-MOD(COUNT(B$2:B2),6) = 0, -6, -MOD(COUNT(B$2:B2),6)), 0))/($C$1/25), 2) * POWER(1 + B2/2, IF(MOD(COUNT(B$2:B2) + 6, 6) = 0, 6, MOD(COUNT(B$2:B2) + 6, 6))/6), 2) * ($C$1/25)
Going down to row 16, it should look like the following:
A16 = 01/01/23
B16 = 9.62%
C16 = 10,792
This is what’s showing on my worksheet.
Cut and paste B2:Bn to B1, which will align the variable rates to the correct months and will also modify your function as follows (in cell C2:Cn):
=ROUND(ROUND(IF(MOD(COUNT(B$1:B1) + 6, 6) = 1, OFFSET(C2, -1, 0), OFFSET(C2, IF(-MOD(COUNT(B$1:B1),6) = 0, -6, -MOD(COUNT(B$1:B1),6)), 0))/($C$1/25), 2) * POWER(1 + B1/2, IF(MOD(COUNT(B$1:B1) + 6, 6) = 0, 6, MOD(COUNT(B$1:B1) + 6, 6))/6), 2) * ($C$1/25)
This works.
I cannot get any of these formulas to work. I have two iBonds, but still just trying to get even ONE to show correct interest. First one was purchased 4/1/22, 10k. Can either of you help?
Chess, for a $10K bond purchased in Apr-22, I get $10,684 through Feb-23 using that formula. Of course, TreasuryDirect will knock off the last three months of interest, so the current value on TreasuryDirect should be $10,436, which is the Nov-22 value.
Try going here: http://eyebonds.info/ibonds/index.html and then click on the April 2022 I Bond link. Then you can see your current holdings (10,684) and also the extended interest out to October 2023 (11,208). You are still on the 9.62% rate until the end of April.
Thanks – that is a great site! I wanted to get this formula to work in my spreadsheet. But I got it now I think.
Very nice!
Now you’ll just need to add a new column for the fixed rate that applies only to bonds purchased during that six-month period and insert something into your function to handle that.
Hi Cheers, I’ve modified your Excel formula to accommodate a fixed interest rate. It was pretty easy. I just had to add two more terms to the POWER function. Your instructions above for setting up the spreadsheet remain the same EXCEPT you’ll need to insert a new column between B and C (insert the fixed rate in C1), which means the amount purchased will be in D1 and the Excel formula in D2 and copied down.
Here’s the revised formula:
=ROUND(ROUND(IF(MOD(COUNT(B$1:B1) + 6, 6) = 1, OFFSET(D2, -1, 0), OFFSET(D2, IF(-MOD(COUNT(B$1:B1),6) = 0, -6, -MOD(COUNT(B$1:B1),6)), 0))/(D$1/25), 2) * POWER(1 + B1/2 + C$1/2 + (B1 * C$1 / 2), IF(MOD(COUNT(B$1:B1) + 6, 6) = 0, 6, MOD(COUNT(B$1:B1) + 6, 6))/6), 2) * (D$1/25)
Cheers,
Please note that I made one other mod to you practically perfect Excel equation by changing $D$1/25 to D$1/25 — you know what I’m referring to — thus making the column relative and not absolute. This will allow folks to track multiple I-Bond purchases of various dates on the same spreadsheet merely by copying and pasting the four columns (Date, Variable Rate, Fixed Rate, Bond Value) to other columns and simply modify the purchase date, variable rates, fixed rate, and original purchase value. BUT, they must all begin in Row 1, since that row is absolute in your excellent Excel equation.
Cheers, you have written a very elegant Excel equation that anyone can use for any I-bond of any value purchased on any date. You know your stuff, Excel-wise.
Bravo Sir.
Thank you so much for this! You’d think TreasuryDirect would be more transparent about the value displayed on their site.
Thank you for this helpful video. I purchased my I bond June 5th 2022 and have yet to see any interest applied in my account. Is that normal?
If you purchased in June 2022, this is not normal. The Savings Bond Calculator shows $1,000 as earning $32 through December. That is subtracting the three-month penalty for redeeming before 5 years.
Make sure you drill down on the “Savings Bonds” hyperlink to get to the bond value – the opening page it will only show the original face value.
Pingback: I Bonds: A not-so-simple buying guide for 2023 | Treasury Inflation-Protected Securities
Having made the exact same investment ($10K in May 2022), and not having a clue why after in December (well after the 6 month, my total only had a $320 increase, I was thrilled to find this perfect explanation. But what still seems wrong (at least to me) is that while researching on treasurydirect, I was lead to believe that withdrawal before 5 years would result in loss of the LAST 3 months of interest. As I expected the past years $9.62% interest to be much less by the time I withdrew, you can see why I’d hoped the interest deducted would be based on the interest rate at the time o of withdrawal. Isn’t that what the “LAST” three months of interest would be? Based on the calculations in the tables shown hear, my lost interest a year from now would be based on the $9.62% in place at the time of investment. No way in the world I could argue with the federal government, but despite the good rate I feel slighted. Am I wrong?
The penalty is on the most recent three months earned. If you bought in May 2022, then the 9.62% interest ended in October. You are now earning 6.48%. If you redeem in May 2023, you will lose three months of 6.48% interest.
OK thanks! So in your example the $320, is $160 less than the “non penalty” $480 number. Just for the sake of understanding, had the interest rate dropped to zero after October, then in another 6 months the $160 reduction would actually become a $0 reduction. (I realize the interest rate actually dropped to 6.48% not zero, and also that the compounding means this number is not accurate to the dollar. But I’m just wanting to cement my “hoped” understand that the penalty will always be based on 3 months of the interest rate that is current.
If the rate fell to zero, and you held until you could redeem in May 2023, the three-month penalty would be zero, since the last three months earned zero.
i use a spreadsheet that calculates the current value of my i bonds. it’s easiest/clearest to write a function that does the calculation, but i did it as a formula for the sake of having it in one place that can be used by people who don’t know how to use scripts in google sheets.
i made a template of the calculator at https://docs.google.com/spreadsheets/d/1J-ymy3ka61PtcziZPqjM-avrYK6fJlF7Uf34yKBI-as/edit?usp=sharing
in particular, the math is in cells C3:C
=IF(ISBLANK(B3), “”, IFERROR(ROUND(B3/25*REDUCE(25, MAP(FILTER(‘historical rates’!B$2:B, ‘historical rates’!A$2:A >= DATE(YEAR(A3), MONTH(A3)-5, DAY(A3))), MAKEARRAY(CEILING(DATEDIF(DATE(YEAR(A3), MONTH(A3)-5, DAY(A3)), TODAY(), “M”)/6), 1, LAMBDA(row_index, column_index, MIN(IFERROR(DATEDIF(DATE(YEAR(A3), MONTH(A3)+6*(row_index-1)+IF(DATEDIF(A3, TODAY(), “M”) < 60, 3, 0), DAY(A3)), TODAY(), "M"), 0), 6))), LAMBDA(inflation, months, POW(MAX(1+inflation+VLOOKUP(A3, 'historical rates'!A$2:C, 3)/2, 1), months/6))), LAMBDA(principal, interest, ROUND(principal * interest, 2))), 2), "? – check rate history table"))
which depends on the 'historical rates' table consisting of columns A: date, B: inflation rate, and C: fixed rate; and the primary tab consisting of A: issue date and B: issue value.
it matches the amounts i see at treasurydirect.gov exactly, which includes bonds purchased 5, and 1 < x 0%. the only thing i’m curious about is what the early redemption penalty is at 4 years and 10 or 11 months (i.e. if it’s a 3 month penalty, or less).
basic steps of the formula:
1. look up interest rates for the life of the bond
2. calculate how many months those interest rates are effective for (i.e. 6 months for all terms except the latest, or possibly except the two latest if within 5 years)
3. calculate the effective interest rate based on steps 1 and 2, and making sure it’s never negative
4. perform the semiannual calculation, rounding at each step
Thanks for the very interesting Excel cell function — LAMBDA, really? — but it’s not nearly that complicated… sigh…
i meant a custom script function would’ve been simple. i know the formula i wrote is an enigma to look at. the only advantage of doing it as a cell formula (as i did above) is that using it only requires pasting that formula into a cell. let me know if you (or anyone) want to see it as a script function, and i’d be happy to author that for you
I found a flaw when using this: If the issue date is 11/1/2021 (exactly) a ? – check rate history displays instead of the correct amount.
hi Kevin, thanks for letting me know. I tried to fix it a couple times but it was tricky, so I changed it to using apps script instead. This only held my attention for several minutes every few months, hence taking 8 months to respond:
https://docs.google.com/spreadsheets/d/15wpraNqXwaGHG-LYQRx2N5rtCbgqp9vwkM3a8Xh5G6I/template/preview
You can click on “Use Template”
Pingback: December newsletter - Glassner Carlton Financial
Pingback: I Bonds vs. TIPS: Right now, it’s clearly ‘advantage TIPS’ | Treasury Inflation-Protected Securities
Pingback: Short-term I Bond investors: Be patient with your exit strategy | Treasury Inflation-Protected Securities
I’m a little confused on how the new rate affects my I bonds purchased in April 2021. Specifically, the .40 base? Somewhere I got the impression that eith the reset I will just receive the 6.48%. Is that true? Or did I misunderstand something?
The new fixed rate does not apply to purchases in April 2021. That fixed rate of 0.0% is permanent and your new composite rate will be 6.48%, beginning in April 2023.
Thank you for clarifying for me.
Very helpful. Thanks. But when calculating for the new rate (6.48% using $27.14 from month 12 for months 13 thru 18) the values do not match the eyebonds.info site for months 2 thru 6 of the 6 month period. I may have an error in my spreadsheet, but if so I can’t find it. The dollar amounts are off by $1 to $2 each month.
I did find a mistake in my spreadsheet. Your approach works.
I do see the eyebonds.info is listing the new composite rate at 6.48%. Is that right?
Thanks again.
I’m seeing 6.89% on that site for the composite rate, which is correct.
Thanks. I was referring to the composite rate for the May 2022 bond. The new .4% fixed rate (and 6.89% composite rate) for the November 2022 bond threw me.
6.48% is correct for the May 2022 bond.
Beautiful. I was just looking at this today because of the 6 month aniv. and changeover and got totally confused by why the value was understated. Of course I googled and chance would have it that I got THE PERFECT ANSWER and explanation right up top. Kudos on this work.
Is there a spreadsheet available that would calculate the value of an IBond portfolio after inputting the purchase dates and bond values? I realize the user would have to plug in the interest rates for each May & November going forward.
Thank you for your articles on this topic.
I am sure some of my financial genius readers have built a spreadsheet like that. However, a good option for everyone else is to use TreasuryDirect’s Savings Bond Calculator: https://www.treasurydirect.gov/savings-bonds/savings-bond-calculator/ . TD says this is for “paper I Bonds only” but it works fine for all I Bonds. But you have to enter a $10,000 purchase in as two $5,000 purchases. I wrote a user’s guide back in 2018: https://seekingalpha.com/article/4179171-step-step-guide-to-using-treasurys-new-savings-bond-calculator
Thank you so much! Too. Infusing to process but you assured me to trust the process! And then showing the balance within the 3 year period makes sense too. Much appreciated!
Nice discussion of the topic. Thanks.
The Treasury Direct FAQ and your article say that the early redemption penalty is the latest 3 months interest. It looks like in practice it is actually the first three months. This is a very big deal given the very high rates at issuance. If rates revert to the mean and I redeem, I would definitely prefer to lose .5% over 2.4%.
It is the last 3 months. Without question.
On what basis do you make the claim that “in practice it is actually the first three months?”
Pingback: Ignore the fixed-rate drama; buy I Bonds in October | Treasury Inflation-Protected Securities
QUESTION
Do the number of days in the month make any difference?
I Bond interest is based on months, not days.
I’m 99% sure that your guess as to what happens when the interest rate changes is incorrect, although it made no difference in your example. Instead of using the rounded value of the $25 I bond at the end of month 6 as the updated baseline for months 7-12, I think you should use the unrounded value. It just so happened that for 7.12%, the rounded value is exactly equal to the unrounded value of $25.89. Not so with 7.13%
Have you seen documentation for this? I’d love to see the exact formula for the 6-month compounding.
No documentation is why I’m 99% sure, not 100% We’ll just have to confirm that it works over a longer time period, but I think this formula works for EVERY month, not just the months when the interest rate changes: Next month’s value=(face amount/25)x(this month’s unrounded value of a $25 bond x (1+next month’s pseudo rate), rounded). Then next month’s interest = next month’s value minus this month’s value. I can send a spreadsheet in reply if you email me.
I have checked my formula against TreasuryDirects’s Growth Calculator, for a $25 bond over 30 years, and interest rates of 2%, 4%, and 6%, and my results agree with their results to the penny. So now I’m 99.99% sure of my formula. The formula you used, using the rounded values of the $25 bond for the 6 month rate updates, was off by pennies in each case. This would mean that despite TreasuryDirect’s assertions, interest is really compounded monthly (because of the pseudo rates) NOT every six months.
Oops. I was 99.9% sure I had it, but I was 100% wrong. Your guess was absolutely right. When a new interest rate takes effect for 6 months, use the rounded value of the $25 I bond at the end of the previous 6 months for the calculations. (I had said to use the unrounded value.) The documentation for this is actually found in the 31 CFR 359.39, where it provides the formula
FV = PV × {[1 + (CR ÷ 2)] ^ (m ÷ 6)},
which is rounded to the nearest cent. The rounded FV for m=6 becomes the PV for the next 6 months, so PV is a rounded number.
Redemption values for I bonds are published online at https://fiscaldata.treasury.gov/datasets/. I corrected my spreadsheet of values for the $25 I bond and was able to verify that my resulting October 2022 redemption values for every I bond series ever issued exactly matched the published redemption values.
Thanks for this update, Tom. It seemed logical that the calculation would carry-forward the rounded amount to create the new baseline. I’m willing to just trust the Savings Bond Calculator to get it right, but it is good to know the formula behind it all.
Tipswatch, thanks for your amazing article. I started making my way through it and don’t understand why in every month for the first 6 months the value increased by $60 except for December. I haven’t made my way through all of the other comments, but maybe someone else noticed it as well, or maybe I just don’t understand it yet. Still, you made something I thought was simple into something less complex, and I thank you.
I think this comes from the effect of the “pseudo-compounding” formula combine with rounding the baseline number. In the first six months, December gets $56 while the other months get $60, and in the second six months May and August get $80, October gets $88 and the other months get $84. In Jennifer Lammer’s YouTube video she showed the monthly increases for a different scenario, and they also varied by a few dollars at times, because of the formula.
For complete generality, formulas need to further round off the interest calculation after multiplying by the face value divided by 25. You can buy I Bonds online in any denomination of at least $25, such as $2,561.35, which is equivalent to 102.454 of the $25 I bonds. If a $25 I bond earns 21 cents in some month, 102.454 times 21 cents is $21.51534, which Treasury Direct would further round to $21.52
Seems like the Savings Bond Calculator (SBC) could be a reasonable alternative for some people in some cases. Possible downsides, depending on one’s situation and preferences are: 1) requires access to the internet; 2) need to go to their website; 3) need to do a bit of data entry on the website and then also data transfer to your own records; and 4) the calculator is limited to using only the denominations that are available when buying paper bonds, so if you have a different denomination you’ll have to do some extra calculations to make it useful. For electronic iBonds at least, for someone who is only interested in the current redemption value (from which they can also easily calculate the current total interest amount), it seems like it would be just as easy or easier to just login to their account and look at the list there. For myself, the one feature of the SBC that sounds like it might potentially be helpful in the future is to create an inventory list of my holdings, but at the present I don’t really have a high enough number of different holdings for that to make sense. Thanks for mentioning this though, Patrick, as I know others have already and will find it to be a helpful tool.
Calculating the value of an I-Bond is so much simpler using a spreadsheet. The magic formula provided by Jennifer and David — with the six-month pseudo-compounding based on the fractional exponent — is correct and produces results that are identical to TreasuryDirect’s calculator, right down to the penny every month. Why do it many times when you need only do it once?
I agree, hoyawildcat, but I’m guessing the initial setup (and any related troubleshooting) can look a bit daunting to anyone who has only a limited knowledge of spreadsheet programs and their formulas. Having said that, I think what you’ve provided here provides a huge ‘shortcut’ for someone like this, giving them a tool / resource they can use to expand their spreadsheet knowledge / skills while also tweaking it into a specific solution for their own needs. Depending on their starting point, they’ll still need to put some time into it, but it will be a lot less time than if they were just starting by staring at a ‘formidable’, ‘mystifying’, and very blank spreadsheet. 🙂
Dustin, I use the Savings Bond Calculator (SBC) because I like to know my monthly interest for each month for the next six months. One need use it only twice a year, when the rates reset. You only have to input the purchase price of the bond and the month and year of the purchase. You can combine bonds purchased in the same month and year. Once you get it set up, it is very easy to get the amount of interest for the next months. I am only interested in the total interest for all my bond holdings. I don’t care too much about interest for an individual bond, although you can see it if you want.
BTW, I checked the SBC using an HP 15C calculator many years ago and it was correct. The SBC is of course a lot easier to use (though somewhat clunky, but hey, it is a government program). I admire your efforts and stamina.
Patrick, that sounds like an approach that definitely works for what you are wanting to accomplish. (I have no doubt the SBC is accurate.) Am I correct in assuming that the denominations of bonds (or combined totals of bonds) that you need to enter always matches an amount that’s available in the SBC’s drop-down menu (i.e. the amounts available for paper bonds)? If so, that would definitely simplify the process. And when you say “once you get it set up”, are you talking about just entering the data in the SBC, or also about some sort of file / spreadsheet you maintain on your own? Thanks for providing additional color in regards to your approach to this.
Dustin, I think sometimes I have to enter a $10,000 bond as two $5,000 bonds, but I don’t think much about it, I just do it. I just make sure the amounts of the bonds all add up to what they should be when I am finished inputting.
“Once I get it set up” is a little unclear. I should have said “once I input my data into SBC”, meaning the bond purchase price and the date of purchase. Then I just change the month and year in the SBC to which month and year I want the interest. SBC gives me the total (principal plus interest), but I simply subtract the previous month from that to get the monthly interest. If you change the month and year in the SBC too far in the future (like 7 months) it conveniently and logically gives an error message. I type in the total interest I get from SBC for each month into Quicken, which keeps track of everything (bank accts, I-bonds, etc.). I have a special row in Quicken just for I-bond interest.
I have maybe 30 or 40 I-bonds, but I combine the $1000 ones that had the same purchase date. Remember I only care about total interest for all my holdings and don’t care to see the interest for each bond, although that is possible. I would say it takes about 15 minutes for the whole process at each rate reset to get interest by month for each of the next six months. In other words, it takes about a half an hour each year. Most of that time is spent inputting the bond info.
I also like to do this to make sure nobody has been messing with my Treasury Direct account (I should probably look more often). There is a part of the web site which gives total principal plus interest for the current date, which I look at quickly to make sure the total matches (I suppose you could look at that once a month to see your interest).
To be clear, I do not use a spreadsheet. I use SBC to generate the interest, and Quicken to record the interest. I have a record of monthly interest back to 2001.
Thanks, Patrick, for taking the time to share how you manage your iBonds. It’s interesting to me to see the different approaches that people take to this. Now all you have to do is convince Treasury Direct to offer a complimentary service that automatically downloads the info you want into your Quicken program each time there’s a rate reset. 😉
Dustin, I wouldn’t hold my breath on that download to Quicken. But just as well. I really only have to type six numbers into Quicken (one for each month) and I only have to do that twice a year. I like the way my approach gives me my future earnings up to six months out, I only have to do it twice a year, I don’t have to mess with a spreadsheet, and it’s easy (easy for me anyway).
As I have noted, I do use the Savings Bond Calculator to track the value of my I Bonds and I only perform updates about once a quarter when I am considering re-balancing my portfolio. It’s a fine tool, and I wrote a guide to getting started for SeekingAlpha back in 2018: https://seekingalpha.com/article/4179171-step-step-guide-to-using-treasurys-new-savings-bond-calculator
This falls under the category of “everyone, including the government, making things harder than they had to be”, and I say this as someone who actually IS a math teacher!
The biggest confusion above seemed to be how to handle the compounding for I-bonds held more than 6 months. And based on some playing around in Excel and comparing it to a thankfully-previously-downloaded I-bond value chart, it seems like you came up with the right idea. The most direct way to do the calculations, for every half-year interval (except the last if it’s incomplete), is to ignore the “pseudo-monthly compounding”, and just do a two-step process.
1. Take the incoming $25 bond value, and multiply it by 1 + the semi-annual growth rate.
2. Round to the nearest cent.
If the final interval isn’t complete, then you need (1+SAGR)^(M/6) as the factor in step 1. If you haven’t held it for 5 years, then just pretend it’s three months ago.
Given that the compounding really only happens every six months, it would make a lot more sense if they treated the interest as simple throughout that interval. That is, if a bond is to accumulate $2.16 of interest in a six-month interval, it gains 36 cents each month. Oh well.
And at the end of the day, what is the end result of this needless complexity? I investigated the value of two $1000 I-bonds, purchased in July 2015 and July 2018, as of July 2022. The true values, which matches my spreadsheet calculations, are $1162.00 and $1104.80. If there was no intermediate rounding, and we just did $1000 * (1+rate1) * (1+rate2) * … etc., the values would be $1161.86 and $1104.65. A difference of literally pennies (and it’s actually a difference in our favor!)
If anyone is interested, I can provide step-by-step instructions for a simple Excel spreadsheet that will show the monthly value of an I-Bond over its 30-year term and also show the redemption value for any month (including the three-month penalty during the first five years).
I would be interested in seeing those, hoyawildcat.
Sorry, can’t do it because my posts are not showing up.
No problem; thanks for trying.
I am posting this for hoyawildcat, since it might be too long for WordPress to handle. I have not tested this at all, but here it is:
Here’s a way to create a simple Excel spreadsheet that will calculate the value of an I-Bond over its 30-year term and show you the redemption value in any month (including the 3-month penalty).
1. We will use columns A through L. In most cases you will only need to enter data or formulas in rows 1 and 2 and then copy-down the columns in row 2. Format column A as a date showing the month and year (i.e. MMM-YY). Format columns B as a percentage with two decimal places. Format columns D through L as currency with two decimal places.
2. In cell A1, enter the first month when the new I-Bond interest rate was set, e.g. May-22 in this example. In cell A2, enter “=DATE(YEAR(A1),MONTH(A1)+1,DAY(A1))”. Copy-down cell A2 through cell A361, which will give you 30 years plus one month of monthly dates.
3. In cell B1, enter the interest rate as of the date in cell A1, e.g. “3.54%” for May-22. In cell B2, enter “=B1”. Copy-down cell B2 through cell B360. In cell B7, enter “7.12%”, i.e. the interest set in Nov-22. In cell B13, enter “9.62%”, the interest rate set in May-23. (You can also enter your guesstimates for future interest rates in cells B19, B25, etc.)
4. Select the month you purchased the I-Bond, e.g. Oct-22 (row 6) in this example. In column C6, enter “1”. In cell C7 enter “=IF(C6=6,1,C6+1)” Copy-down C7 through C360. Note that the numbers range from 1 through 6 and then reset. We will use these values in the magic formula for the numerator of the fractional exponent, e.g. 1/6, 2/6, and also for the semi-annual compounding.
5. In cell D6, enter “$25.00”. In cell D7, enter “=IF(C7=1,E6,D6)”. Copy-down C7 through C360. Don’t worry about the calculated values for the moment.
6. In cell E6, enter the magic formula: “=ROUND(D6*(1+$B1/2)^(C6/6),2)” Copy-down E6 through E360. (Note that this will reset the values in column D and also show the semi-annual compounding.)
7. In cell F6, enter “=E6-D6”. Copy-down F6 through F360. (This is the cumulative interest during each six-month period.)
8. In cell G6, enter “=IF(C6=1,F6,F6-F5)”. Copy-down G6 through G360. (This is the interest earned each month.)
You now have all the info you need to calculate the monthly value of your I-Bond. For a $10K bond, you simply need to multiply the values in rows D through G by 400 (i.e. 10000/25). We’ll do that now.
9. In cell H6, enter “=D6*400”. (You can use a constant for the multiplier if you want to play with the bond value. For example, enter the bond value (10000) in cell N2. In cell N3, enter “=N2/25”. Cell N3 will contain the multiplier. You can use that by entering “=D6*$N$3” in cell H6. Be sure to enter an absolute cell address — $N$3 — so that when you copy-right and copy-down the cell address of the multiplier will remain constant.)
10. Copy-right H6 through K6. Copy-down cells H6 through K6 to H360 through K360. You now have the bond value and interest earned for each month of its 30-year term.
11. We will now calculate the actual redemption value in each month including the 3-month penalty during year the first five years. In this example, the I-Bond was purchased in October 2022. Therefore, the first month you can redeem it is October 2023. In cell L18, enter “=I15”. This was the bond value as of July 2023. Copy-down L18 through L66, which corresponds to October 2027.
12. In cell L66, enter “=I65”. Copy-down L67 through L361. Column L now contains the redemption value of the I-Bond by month.
13. For better readability, insert a new row above row 1 and enter column headers in the newly created row.
Thanks.
Ok, I was game. I followed your instructions. It’s an elegant way of doing things. Just a few things I noticed:
1. Steps 3 & 4: The interest rates are off when the example investment begins in Oct-22. There’s one month at 3.54%, then it switches to 7.12%.
2. Step 4: In cell C6 (not column).
3. Step 6: The magic formula is incorrect. It should be (C6/2), not (C7/2).
4. Steps 11 & 12: The L66 and L67 formulas seem off.
🙂
1. Steps 3 & 4: I don’t see that. Cells B1 through B6 should be 3.54% and cells B7 through B12 should be 7.12%. If they are then the interest is calculated correctly (after you fix the magic formula as described below).
2. Step 4: Yes, it should be “cell C6.”
3. Step 6: Sorry, that was a typo. The magic formula in cell E6 should be “=ROUND(D6*(1+$B1/2)^(C6/6),2)”. Enter that in E6 and then copy-down E6 to E360.
4. Steps 11 & 12 are correct. You don’t earn any interest in the redemption month.
Why do you guys keep going over this for less than a price of a hamburger over 6 months. Its actually down to pennys. So is it safe to say that if I have a 10k I bond and it pays 9.62 for 12 months that at the end of the term I should have in my account 10,962 minus about 240 for the prior three months for a total of 10,722 give or take a few dollars. I mean you could figure monthly without all this back and forth.
Mike, I’m a retired software engineer. Old habits die hard.
Ok, I have the interest rates set as you instructed. But, in Step 4, you use Oct-22 as the purchase month. So all the formulas are set at line 6, which is also the last 3.54% line. If I leave the interest rates as is, things are off. I would need to adjust the rates to the purchase month?
In Step 11, you say to copy something down through L66, but in step 12, you changed the formula for L66. Is that correct?
Jack, did you enter the new interest rates for Nov-22 and May-23 as described in step 3 ?
Step 11 provides the redemption value for years two through five with the three-month interest penalty. Step 12 provides the redemption value after five years with no interest penalty. Note that you will not earn any interest in the month that you redeem the bond. Jennifer’s video discusses this in some detail.
Hi. Can you clarify in Step 3 why you say the interest rate as of May 2022 is 3.54% , the interest rate set in Nov 2022 is 7.12%, and May 2023 is 9.62% ?
When I look at a table of previous and current rates, they show as Nov 2021 – Apr 2022 7.12%, May – Oct 2022 9.62%, Nov 2022 – Apr 2023 as 6.89%.
I’m trying to understand why in my interest rate column I wouldn’t use 9.62% for May 2022 and why I should use 3.54% as your example.
I bought my I-BOND in Mar 2022. Wouldn’t my excel sheet therefore begin Mar Apr 2022 @ 7.12%, then May thru Oct 2022 @ 9.62% and finally Nov 2022 – Apr 2023 as 6.89%?
I’m totally lost why (I’m sure) I’m not looking at this correctly. Help pls!
Thanks
Not sure exactly what you are asking, but if you bought in March 2022, you got a full six months of 7.12% and then in September 2022 you began earning six months of 9.62%. The new variable rates begin on a six-month schedule that starts in your month of purchase. … And you will never earn the 6.89%, because that includes the 0.40% fixed rate for I Bonds bought from November 2022 to April 2023. Instead, you will earn 6.48% for six months.
Thanks for the reply. What I was asking was in reference to what hoyawildcat said (but posted by you on their behalf) in their example of how to set up the Excel sheet with their method.
Step 3 says:
“In cell B1, enter the interest rate as of the date in cell A1, e.g. “3.54%” for May-22.”
But the rate for May-22 was 9.62%
Then again, the example given for v Cell B7 is:
“In cell B7, enter “7.12%”, i.e. the interest set in Nov-22. ”
But the rate in Nov-22 was set at 6.83%
Clearly I’m missing something fundamental here. But I can’t see what that is.
Is it not true that the rate from May -22 to Oct 22 was 9.62%? (According to a historical table I’m looking at). I’m having trouble understanding why hoyawildcat says to put 3.54% for May 22 and copy that down to Cell B7 in their example.
Hopefully my question is clearer? Thanks!
Sorry, that was a typo. It should have read ‘In cell B1, enter the interest rate as of the date in cell A1, e.g. “3.54%” for May-21’ and ‘In cell B7, enter “7.12%”, i.e. the interest set in Nov-21.’
Thanks for pointing it out.
Ah thank you so much for the reply! I was all coffee’d up ready to tackle your awesome detailed guide for a comprehensive Excel sheet and I got stuck on the interest rate/date example. Feel much better that it was just a typo! 🙂
One other question if possible:
If I purchased I-Bond in March 2022, that means I get the 7.12% rate. But is that only lasting for Mar & April 22 and then switches to the new rate set in May 22 @ 9.62%? Or should I be calculating 6 months at 7.12% (Mar 22 – Aug 22) and THEN start using the new rate in Sept 22, for the next 6 months, even though it was set in May?
Apologies for the dumb question! Thanks
Each interest rate lasts for six months, regardless of when you purchased the I Bonds during that six-month interest rate timeframe. So, if you purchased in March 2022, then you got the 7.12% (annualized) rate for six months, through August 2022, and in September 2022 it was raised to 9.62% for the next six months, etc.
Thanks for helping to get this posted, David. And thanks, hoyawildcat, for investing your time in sharing your Excel skills with us in this way. I am definitely going to be saving these instructions in case I ever decide to use this type of setup, and also as a practical tool / project for increasing my own ability in using spreadsheet software. As a sidenote, it’s interesting that working with spreadsheets is not all about knowing the functions and formulas — there’s a fair amount of design work involved, and it’s usually worth putting time and thought into coming up with a good design for whatever solution is needed. I guess in that sense it’s a bit like software engineering.
PLEASE NOTE: There’s typo in the magic formula in step 6. “(C7/6)” should be “(C6/6)”.
Here’s the correct instructions:
6. In cell E6, enter the magic formula: “=ROUND(D6*(1+$B6/2)^(C6/6),2)” Copy-down E6 through E360. (Note that this will reset the values in column D and also show the semi-annual compounding.)
Sorry for the mistake.
David fixed the error in step 6 of the original instructions.
No problem, hoyawildcat. I’ve been saving the notification emails of the follow-up comments here. For some reason, I don’t get notifications on all of them, but I can always come here again to see if I’ve missed anything. Thanks to Jack for his testing / reporting, and to you and David for your prompt corrections.
@hoyawildcat, I’m using this set of instructions to set up a spreadsheet, but I’m finding that with Step 11, the redemption value figures in column ‘L’ are off by one row, based on comparison with the calculations in my original spreadsheet and confirmed for at least one date with Treasury Direct’s values. In looking at it, I think the formula instructions in Step 11 should read “In cell L18, enter “=I14”.” Could you check this out and confirm? I think the ‘tricky’ part is that: 1) your formulas reflect the amount of interest *earned*; 2) the interest earned is not *paid* until the first of the following month; and 3) no interest is earned in the month of redemption. So with your spreadsheet setup three rows need to be excluded in order to exclude the three months of earned interest representing the penalty. Using your cell references that would mean: 1) row 18 is excluded because no interest is earned in the month of redemption; 2) rows 17, 16, and 15 should be excluded for the penalty; and 3) cell I14 should be used for the redemption value in L18, since this is what would hypothetically show up in L15 (i.e. three rows / months previous to L18) if there were no holding period limitations or penalty. Hope that all makes sense. Let me know what you think.
For my setup, I also found it helpful to calculate the penalty amount, which could then be used to adjust the current value for bonds held less than five years. The mental approach I used for this was to calculate the total interest accrued for at least the previous three months and then subtract any amounts from months prior to that whose accrued interest would no longer be included in the penalty. This is a bit of a different approach than this article uses, which is to add the accrued interest for a month in whichever month it is shown by Treasury Direct (TD), but they both give the same result. I’m obviously biased ( 🙂 ), but I like my approach a bit better because it ‘feels’ like it more clearly represents what TD actually does when it applies the penalty. However, I do recognize that the associated calculation(s) / formula(s) are a bit more complex. There may be more elegant ways to do it, but following are some example formulas for calculating the penalty amount.
Example #1:
* Bond Details: $1500 principal, purchased in March 2022, 7.12% initial interest rate, results will show penalty applicable in September.
* Prerequisite: Use the formula =ROUND(25*(1+0.0712/2)^(6/6)-25,2)*1500/25 in the cell of your choice (I’ll use F8) to calculate the total interest accrued, as of September. (This simplifies the process because now I can use ‘F8’ in the penalty-related formula to include this formula, including any future changes to it.)
* Formula for penalty amount: =F8-(ROUND(25*(1+0.0712/2)^(3/6)-25,2)*1500/25) (English translation: 1) I’ve determined that I want to exclude the first three months of interest in this six month period, so I use the second portion of the formula [with the ‘^(3/6)’] to calculate what that amount would be. 2) Then, I subtract this amount from the result of the formula in F8, which uses the ‘^(6/6)’, which then gives me the amount of interest accrued in the last three months of the period, which is the penalty amount.) (Note that this specific formula is one that can be used to test whether your ‘ROUND’ function is working as expected. If it’s working, the result is 27.00; if not, it is 26.93.)
Example #2:
* Bond Details: $1500 principal, purchased in June 2022, 9.62% initial interest rate, results will show penalty applicable in September.
* Prerequisite: Same as above, except use the formula =ROUND(25*(1+0.0962/2)^(3/6)-25,2)*1500/25 .
* Formula for penalty amount: =F8-(ROUND(25*(1+0.0962/2)^(0/6)-25,2)*1500/25) (English translation: 1) I’ve determined that I don’t need to exclude any months of interest in this six month period, so I use the second portion of the formula [with the ‘^(0/6)’] to reflect that. [This may seem unnecessary because it’s the same effect as subtracting ‘0’, but I want to preserve the structure of the formula for future updates to it.] 2) Then, I subtract this amount from the result of the formula in F8, which uses the ‘^(3/6)’, which then gives me the amount of interest accrued in the first three months of the period [i.e. the same amount as what’s in ‘F8’], which is the penalty amount in this case.)
* The main value of this example is to show that ‘^(0/6)’ can be used when you don’t need to subtract any accrued interest (i.e. when you’ve only accrued interest for three months or less in a particular period).
Example #3:
* Note that I won’t be able to check / test this formula until October, but I think it ‘should’ work. 🙂
* Bond Details: $1500 principal, purchased in March 2022, 7.12% initial interest rate, 9.62% subsequent rate, results will show penalty applicable in October.
* Prerequisite 1: Use the formula =ROUND(25*(1+0.0712/2)^(6/6)-25,2)*1500/25 in the cell of your choice (I’ll use F8) to calculate the total interest accrued at the 7.12% rate.
* Prerequisite 2: Use the formula =ROUND(25.89*(1+0.0962/2)^(1/6)-25.89,2)*1500/25 in the cell of your choice (I’ll use F9) to calculate the total interest accrued at the 9.62% rate.
* Formula for penalty amount: =F9+F8-(ROUND(25*(1+0.0712/2)^(4/6)-25,2)*1500/25) (English translation: 1) Because the formula structure is preserved in the section using the 7.12% rate, I’ve simply added ‘F9’, which represents the one month of interest accrued at the 9.62% rate. 2) I’ve determined that I want to exclude the first four months of interest in this six month period, so I use the second portion of the formula [with the ‘^(4/6)’] to calculate what that amount would be. 3) Then, I subtract this amount from the result of the formula in F8, which uses the ‘^(6/6)’, which then gives me the amount of interest accrued in the last two months of that period, which is the part of the penalty amount at the 7.12% rate.) 4) Once this amount gets added to the ‘F9’ amount, this results in the total penalty amount.
* The main value of this example is to show how the penalty amount can be calculated when it involves two different six-month holding periods.
Additional notes:
* Even though you need to adjust the baseline amount in the formulas when entering a new six-month period (eg. 25.00 to 25.89), there is no need to change the ‘scale-up’ portion of the formula (eg. ‘*1500/25’) because that ratio will stay the same and give the same result whether you adjust it or not.
* If you are wanting the formula to give a result that includes the principal amount, you can just delete the part of the formula that subtracts the baseline amount (eg. ‘-25’ or ‘-25.89’). Alternatively, if using the formulas mentioned above in Example #1, and assuming that the principal amount is in cell F7 and the penalty amount is in E8, then you can use the simple formula =F7+F8-E8 to get the total current value for a bond. (If using this simpler formula, you just need to remember that the principal amount [represented here by ‘F7’] will be reset at the beginning of each new six-month period.)
* Obviously these formulas will become ‘obsolete’ at the beginning of each month, but once you have them in place, it shouldn’t take too much time to tweak them whenever you want to update / check current values.
* Because I am mainly interested in current values, I just use one row in my spreadsheet for each six-month period of accrued interest, tweaking the formula as necessary within those six months whenever I want to update the current value.
Some may find this to be way too much detail and too complicated; others may be thinking “There’s a lot simpler way to do this; just use this function / formula…”, etc. But here it is, in case others might find it helpful. 🙂
Dustin, I love your passion and thank you for your help. For most people, I think, just understanding how the Treasury does its calculations should be enough, and that the calculations are accurate. It can be annoying to see amounts varying by a few dollars from what you think is right. I use the Savings Bond Calculator a few times a year to update values, without worrying if the information is accurate.
You’re welcome. Yes, that makes sense; I noticed that from some of the other comments as well. 🙂 All the best.
As I mentioned before, just use the Savings Bond Calculator. I use it just twice a year, when the rates are reset. This will calculate your interest for each month out to six months. It will tell you when you can’t go any further. It is accurate and easy to use.
I tried out your Example #1. You put a lot of work into it and I was game to give it a go.
Anyway, yes, it works the way you did it and probably for the way you built your table. And like Jennifer says, joy! However, if a person sets up their table the same way David did, which I did, then a person could just subtract what “TD shows” from the “Value of investment.”
For instance, looking at David’s “$10,000 I-Bond purchased Nov 2021” table above. If a bond was cashed in on May 4, 2022, the amount received would have been $10,176. Just subtract that from the “Value of investment” of $10,356 to arrive at forfeited interest of $180.
David’s months are set up as 1 day after month’s end, so actually the 1st of the following month. If the bond was cash in on May 4, the figures for April would have been used (in his table).
If I person didn’t want to set up a table, your formulas work well on their own (as long as one remembers to change certain values within the formula) for finding the amount of the interest penalty.
Thanks for sharing your experience with it, Jack, and I agree with what you said. I already had my spreadsheet set up before I came across this article, so that’s what influenced me in this direction. And thus, the reason I wanted to calculate the penalty was to use that amount in a formula to calculate the value Treasury Direct would show, so a bit of a chicken-and-egg scenario when comparing it with the tables here. 🙂 Also, the tables that David and Jennifer use in their presentations are great for their purpose of illustrating how the calculation is done as you move through time. However, for record-keeping purposes, the approach is a bit cumbersome, since you would need to have six rows for each six month period rather than just one. (Although if someone wanted to do all the data entry for each month, they could then just hide the first five rows at the end of the six-month period to lessen the amount of scrolling needed.) But I guess it all depends on what someone’s goal is, and what feels most intuitive to them for their situation, etc. How do they say, “There’s more than one way to skin a cat.” 🙂
OK just a nit: your statement: “In the case of the November 2021 purchase, that $10,000 I Bond has actually earned $10,856” It didn’t EARN $10,856, actually it EARNED $856. It is now WORTH $10,856. Sorry, as an ex-engineer, I just can’t help myself :}
Excellent point. Fixed.
FYI, readers: Thanks to your great feedback in these comments and emails, I have updated this article to include the formula used to round the “Cumulative $25 bond value” column. If you see any problems with that, let me know!
Not sure the new formula works. I substituted it for what I have, and I’m back to being off $-1.39. Is it possible the ROUND function has to be at the beginning of the formula, because that’s what works for me. Like this: =ROUND(25*(1+0.0962/2)^(1/6),2).
I’m at best a dabbler in Excel and have little idea of what I’m doing. But I managed to get my numbers to exactly match yours. As Jennifer might say, that gives me joy.
Yes, David, I think Jack’s right. I’m pretty sure the effect of ‘+ROUND(0,2)’ in your formula is to just add ‘0’ (i.e. ‘plus the number ‘0’ rounded to two decimal places’). Perhaps it ‘worked’ again for you because your sample calculations don’t need the rounding to be done, not sure. Another tidbit from Jennifer’s video that was quite helpful for my setup was how to figure just the interest portion, which you can do by adding ‘-25’ at the end of the basic formula (to back out the principal amount), like this: =ROUND(25*(1+0.0962/2)^(1/6)-25,2) . And then if you want to put everything in one formula to figure the total scaled-up interest amount, you could use this (for a $1,500 bond): =ROUND(25*(1+0.0962/2)^(1/6)-25,2)*1500/25 . And if you wanted it to include the principal amount as well, just delete the ‘-25’ that was added, etc. Hope that helps a bit. 🙂
This is great, and thank you all. When I can get back to my computer I will make this fix. The reason my 400x calculations worked was because I just re-entered the dollars/cents number from the $25 column into the next equation x 400, so I was locking in the rounding by doing that. My wife (a former CPA) is way, way better at Excel than I am.
Hey, thanks for explaining that. I did wonder how you got the correct answer without seeming to use the ROUND function.
Looking forward to your post about the upcoming 5yr TIPS.
That makes sense. I had considered that as one possible solution to locking in the rounding, but decided I wanted something more automated to save time in data entry, since there’s a chance I’ll be wanting to use this spreadsheet setup for the long-term. In regards to spreadsheet programs like Excel, all I have to do is look at a list of all the functions that are available, and then I realize how much I don’t know about the various things that the program can do. It’s nice that these programs come with ‘Help’ info and you can usually find help via an online search as well, although it can take some time (at least for me) to wrap your head around what a particular function does and how it’s meant to be used. For me, when I’m trying to figure out something new, the biggest step is trying to determine whether the program can actually do what I want it to do, and then assuming it can, trying to figure out which function(s) will get me the result I want.
Excel has a very rich set of functions that can do practically anything you want. (In my opinion Excel is Microsoft’s best product.) The only time I ever had to write my own Excel VBA functions was to calculate MAX and MIN using absolute values, i.e. when both positive and negative numbers were involved. (I wanted to calculate the MAX and MIN variance from zero, irrespective of sign.) There’s no way to do that using built-in Excel functions, so I wrote my own — MAX_ABS and MIN_ABS — which required loading the data range into an array and stepping through it. MAX_ABS was pretty simple but MIN_ABS was somewhat trickier.
Interesting. From your comment, I can tell that you are many miles ahead of me in your spreadsheet program knowledge and understanding. 🙂 (I use LibreOffice’s Calc, but I think most things are probably comparable.) The thing I like best about your comment is that Excel makes it possible for you to create your own functions as necessary — in my mind, that kind of flexibility in a piece of software adds a lot of value.
Thank you for your help!
Thanks for including us in your article David. I’m glad we found one another – I’m enjoying all your TIPS insights. Jennifer
Thanks to you as well, Jennifer, for the time and effort you put into your video on this. I actually found it helpful to see multiple ways of explaining the calculations, the basis for them, and slightly different formulas to reach the same result. That all helped me figure out the ‘guiding principles’ well enough to be able to create / tweak my own set of formulas that work for me.
👍 Glad you’re sorted Dustin – it’s a great joy in life when your spreadsheet works out the way you want it to (for us anyway)!
Thank you to David for introducing me/us to Jennifer Lammer! I always look forward to settling in and watching Diamond Nestegg’s YouTube videos and have found them to be super helpful.
At least for my account, and even for the calculator example you show, Treasury Direct doesn’t round to the nearest whole dollar when they report the current value. (All of my current values reported show cents.) When I checked some of your $10K bond examples though, the math for those always worked out to an answer that was a whole number (so no need to show cents). So maybe that’s why you think they do that rounding? Or am I missing something?
It is, however, important to make sure that you round the final amount you’ve calculated off of the $25 base-line before you go on to use that amount in any following calculations; otherwise, you’ll sometimes be off by a few cents here and there. If using a spreadsheet program like Excel, this can be accomplished within a formula by using the ‘ROUND’ function.
Excellent point, and this should have been obvious to me, because my Savings Bond Calculator amounts did show cents, which I proceeded to eliminate by multiplying by 10. You are correct that the rounding takes place on the $25 baseline, to the nearest cent. Thanks for noticing this and I am correcting my article. (All the calculations remain the same, fortunately, since I was already rounding the $25 baseline number). For a $10,000 I Bond, there will never be cents in the final result, because of the factor of multiplying by 400. But that isn’t true for a $1,000 I Bond, with a factor of 40.
You’re welcome. I found it very helpful to work my through your article as well as the linked video (two different angles to the same thing), and that was the only thing that didn’t make sense to me. The time and effort you put into this post to help us all understand how the calculations are done is much appreciated.
*work my way through
Rounding the interest on a $25 bond to two decimal places was the first thing I did before multiplying by 400. There are no fractional pennies.
Thank you for mentioning that ROUND function because for the life of me I couldn’t match David’s Value numbers. Once I added ROUND, I could exactly match his figures.
You’re welcome, Jack. I had that same problem when I was trying to get my results to match the current values reported by Treasury Direct. It can be a bit of a mystery, especially if you have your formatting set to only show two decimal places because it definitely *looks* like it’s already rounded, but the unrounded amount is lurking in the shadows, waiting to pounce on you when you use that value in another calculation. 🙂 Luckily, I remembered encountering this effect in some other contexts. I had a memory that the ‘ROUND’ function existed, but hadn’t used it much, but it only took me a few minutes to research how it is meant to be used, and then was quite delighted to see that it was the final piece of the puzzle, at least for those of us that are interested in getting that exact match. 🙂
Imo, the Treasury Dept should be required, for purposes of clarity and transparency, to publicly post the sequence of formulas they use to arrive at their calculations. Other people should be able to duplicate their results. I can duplicate the interest on most of my other investments, my mortgage, etc. There’s nothing proprietary or top secret about it, so I don’t get why it isn’t publicly available.
Even when I try to duplicate the interest on very simple T-bills, I’m always off a few cents. In my view, I should be able to duplicate it exactly down to the penny. That is the simplest of simple formulas, and my result is always different from the Treasury’s result. It shouldn’t be.
If you use the equation provided by David and described by Jennifer then it works down to the penny. It’s actually pretty elegant albeit somewhat primitive (based on $25 bonds).
I suspect that the reason the Treasury Department isn’t more forthcoming about the equations is that the original computer code was probably written in COBOL, of which there are very few surviving practitioners, so no one at Treasury understands it. Your government at work.
Thanks for the info and the link to Jennifer’s video. The pseudo-compounding equation with the fractional exponent actually simplified my spreadsheet. More importantly, my numbers are now completely accurate.
I’m a math geek and played around in Excel to make it spit out the answer for me so that I can play a “what if” scenario (ie what if the next interest rate is 7.0% APR?)
All I did was take the original amount per six months (ie $10,000 to begin with, $10,356 the next six months etc), multiply it by the APR and divide by six to give me a monthly amount.
So… ($10,000 x 3.56%)/6 = $59.33 per month. Next interest will be ($10,356 x 4.81%)/6 = $83.02 per month
So not exact, but is off no more than $1 or less. First month they gave me $60 as opposed to $59.33, but only gave $296 as opposed to my $296.67 calculation. I know they only go by the dollars and not cents, but I was surprised that they rounded up to $60 the first month and down the others. I didn’t lose sleep over it.
That’s the way I’ve been doing it anyway.
Thanks for the article David. When I use the Treasury Direct calculator, I input my electronic bonds by putting TyDirect in the serial number space to generate a report for all of my savings bonds, so you can bend them in there.
I also use the calculator this way, to list all my I Bonds (and a couple remnant EE Bonds). When I create a new listing, I use the serial number space to note the fixed rate, such as 0.0% or 0.2%. And for my account (versus my wife’s) I make it DAVID: 0.0%. The calculator is a great way to see your total value, and yes, it works fine for both paper and electronic I Bonds. I wrote a guide back in 2018: https://seekingalpha.com/article/4179171-step-step-guide-to-using-treasurys-new-savings-bond-calculator
Pingback: Don’t go ballistic over the way TreasuryDirect reports I Bond interest | Treasury Inflation-Protected Securities
So is it safe to say that if I have a 10k I bond and it pays 9.62 for 12 months that at the end of the term I should have in my account 10,962 minus about 240 for the prior three months for a total of 10,722 give or take a few dollars. And if I cut that figure in half thats how much my account should have in 3 months. Does this work or no?
To simplify this, you could just take the base inflation rate for the 9.62%, which was 4.81%, so you’d earn $481 in six months and one half of that is $240.50. That is going to be close. But unfortunately, the correct answer is $236. That is the effect of pseudo-compounding, which causes the return to build over the six months. After the full six months you’d have $480, and that is still off by $1 because of rounding. Isn’t this fun?
So to me thats a heck of alot easier than attempting to figure out that other math. And going in you realize that the next 6 months would produce those extra few bucks I mean what more could you ask for right.
“Two trains are on same track and they are coming toward each other. The speed of the first train is 50 mph and the speed of the second train is 70 mph…”